Energy Incidence Criterion (EIC) is a key concept in EDCA definition, as it determines how energy spot and cell interact to keep the CA running. In order to make this exposition as simple as possible, it will be used the 2-dimensional binary special case of EDCA. All thoughts expressed here can be easily extrapolated to higher dimension lattices and more general sets of cell states.
The main idea about EDCA dynamics is easy to catch: a cell changes its state only when it is covered by a spot, and this spot is uniquely assigned to the cell. That means, the spot may be covering several cells, but it will participate in the transition of only one of them. The rest of the cells will remain unchanged. Obviously, the selection of which cell will suffer the state change at each step is decisive for the CA performance. By the other side, it may occur the situation when many spots are competing for one cell, and certainly, that cell will change it state, but, which of the spots will the responsible? At first sight, it may appear to be not very important, but it is. If the selected spot happens to be the only covering a second standing near (or far) cell, that cell will lose its spot and the possibility of making its transition. That means, the EDCA dynamics will also depend on which spot is selected at every step.
Let’s define the enabling relationship between spot and cell: if a cell is covered by a spot and the sign of the spot is equal to expected cell´s change, it is said that the cell is enabled by the spot. It means that positive spots can enable cells about to be born, while negative spots can enable cells waiting for death.
Let 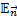 be the set of spots enabling cell
be the set of spots enabling cell 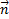 .
. 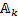 is the set of all cells enabled by spot
is the set of all cells enabled by spot 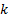 .
. 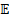 is the set of all spots enabling at least one cell, where
is the set of all spots enabling at least one cell, where  the set of all enabled cells. Sets
the set of all enabled cells. Sets 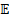 and
and  form the bipartite weighted graph
form the bipartite weighted graph  , where edge weights represent the enabling relationships between sets
, where edge weights represent the enabling relationships between sets 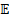 and
and  .
.
Conflictive situations can arise here when a spot covers many cells, or an exceeding number of spots is willing to be assigned to a cell. To resolve these conflicts, graph 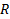 is transformed into a collision free Assignation Graph
is transformed into a collision free Assignation Graph 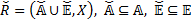 where
where 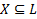 constitutes a matching.
constitutes a matching.
Thus Energy Incidence Criterion is the transformation 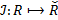 that defines assigned (selected for updating) cells and spots from enabling graph
that defines assigned (selected for updating) cells and spots from enabling graph 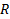 . Inclusion of cell
. Inclusion of cell 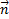 and spot
and spot 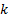 in sets
in sets 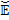 and
and 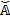 respectively, determines how their next states and values are calculated.
respectively, determines how their next states and values are calculated.
The easiest way to establish an effective selection criteria between cells and spots is to assign a unique number to each cell and each spot. This way, a strict order of assignment is developed: spots are checked by the established order and, for each of them, it is chosen the cell having a greatest number of those located in spot´s coverage zone.
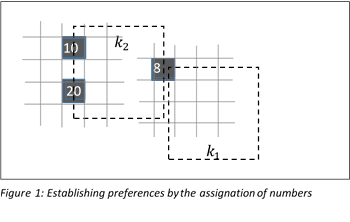
Figure 1 shows the application of the Energy Incidence Criterion in a group of cells and spots that present conflicts of allocation. The conflict between  and
and 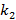 for the cell with number 8 is resolved by assigning the cell to
for the cell with number 8 is resolved by assigning the cell to  because of its lower index. Then the spot
because of its lower index. Then the spot 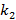 is assigned the cell with number 20 (greater than 10).
is assigned the cell with number 20 (greater than 10).
When modelling physical phenomena, we can take advantage of the Energy Incidence Criterion for inducing a particle-like motion of cell patterns. A pattern, as a conglomerate of cells and spots that display some dynamical behavior as individual entity, can be used to model the dynamics of physical bodies. The control of pattern motion is achieved by the creation of privileged zones on the cell space (lattice anisotropy), or within the coverage zone of the spots (spin vector).