EDCA–Quantum Entanglement Analogs
(1) Single-Spot Nonlocal Collapse and (2) Correlated Spot-Pair Emission
with a CHSH-Style Protocol
Abstract
Energy-Driven Cellular Automata (EDCA) separate logical readiness from physical transition: a lattice site may satisfy a local transition rule yet remains unchanged unless an energy quantum (a spot) arrives. Spots propagate as wavefront shells and collapse when intersecting ready sites; collapse occurs at exactly one site selected from a candidate set distributed across the shell. This structure yields an EDCA-native nonlocal state update: when collapse occurs at one location, all other candidates on the same wavefront instantly lose eligibility for that spot event.
This article presents two EDCA analogs of quantum entanglement. Approach A models single-spot nonlocal collapse: a delocalized wavefront intersects two distant ready clusters, and collapse in one cluster instantaneously conditions the global state of the other. Approach B introduces correlated spot-pair emission, producing Bell/CHSH-style correlations between outcomes at two distant stations whose measurement “settings” are implemented by local readiness/density masks.
1. Introduction
EDCA extends classical cellular automata by introducing an explicit energy layer: matter evolves according to local readiness conditions, but transitions require the arrival of energy carried by mobile entities called spots. A spot expands as a wavefront shell and may collapse at any tick when it intersects a transition-ready site. When multiple sites are ready simultaneously on a shell, a selection rule resolves collapse at a single site based on wavefront geometry, spot-attached spin, polarity, and dynamic allocation density ρ(x,t).
We propose two complementary entanglement analogs: (A) single-spot nonlocal collapse and (B) correlated spot-pair emission.
2. Minimal EDCA Constructs Used Here
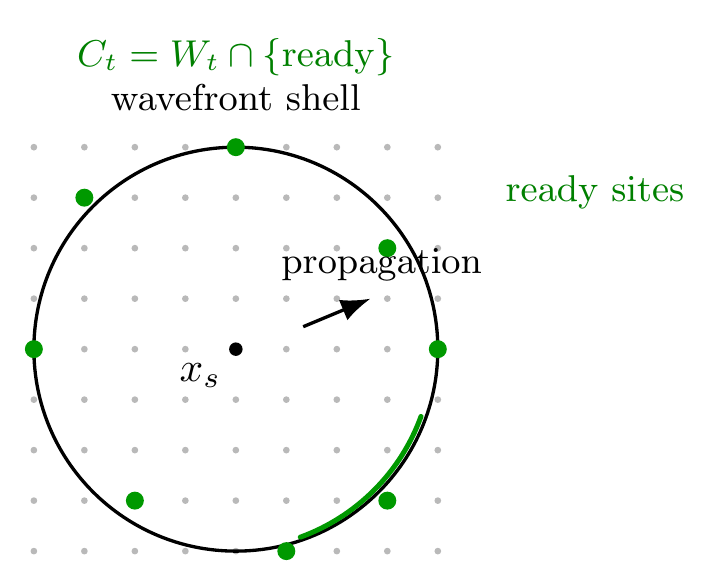
2.1 Wavefront shells and shell sharpness
A spot emitted at source xs defines a wavefront radius r(t) and a shell band Wt = { x : ||x − xs|| ∈ [r(t) − δr, r(t) + δr] }. The shell thickness δr is governed by a sharpness parameter λ.
2.2 Candidate set and exclusive collapse
Let ready(x,t) be the readiness predicate. The collapse candidate set is: Ct = Wt ∩ { x : ready(x,t) }. When Ct ≠ ∅, collapse occurs at exactly one site X ∈ Ct. This implies exclusivity: if X collapses, every other candidate does not collapse for that spot event.
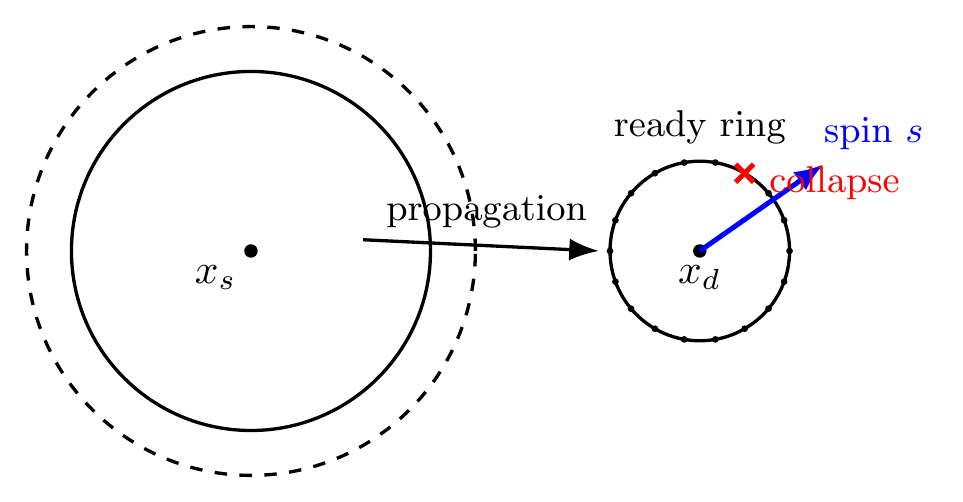
2.3 Spin, polarity, and density bias
Each spot carries a fixed spin vector s, a polarity p ∈ {+,−} that favors or disfavors alignment, and a polarity flip rule upon interaction. Dynamic allocation density ρ(x,t) may also bias collapse selection.
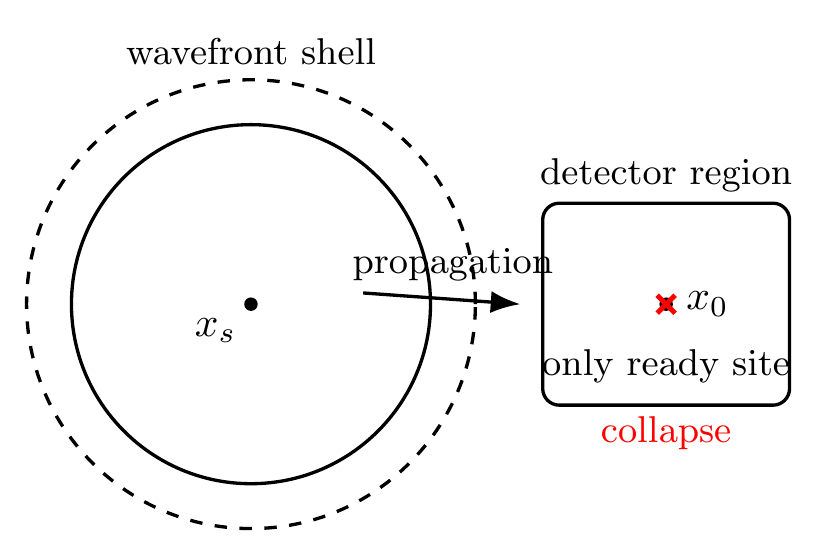
3. Geometric Intuition: Candidate Sets and Station Readout
A wavefront defines a distributed candidate set on a shell. Distant candidate regions can coexist simultaneously. Detector geometries can map collapse location to discrete outcomes.
4. Approach A: Single-Spot Nonlocal Collapse (Entanglement Precursor)
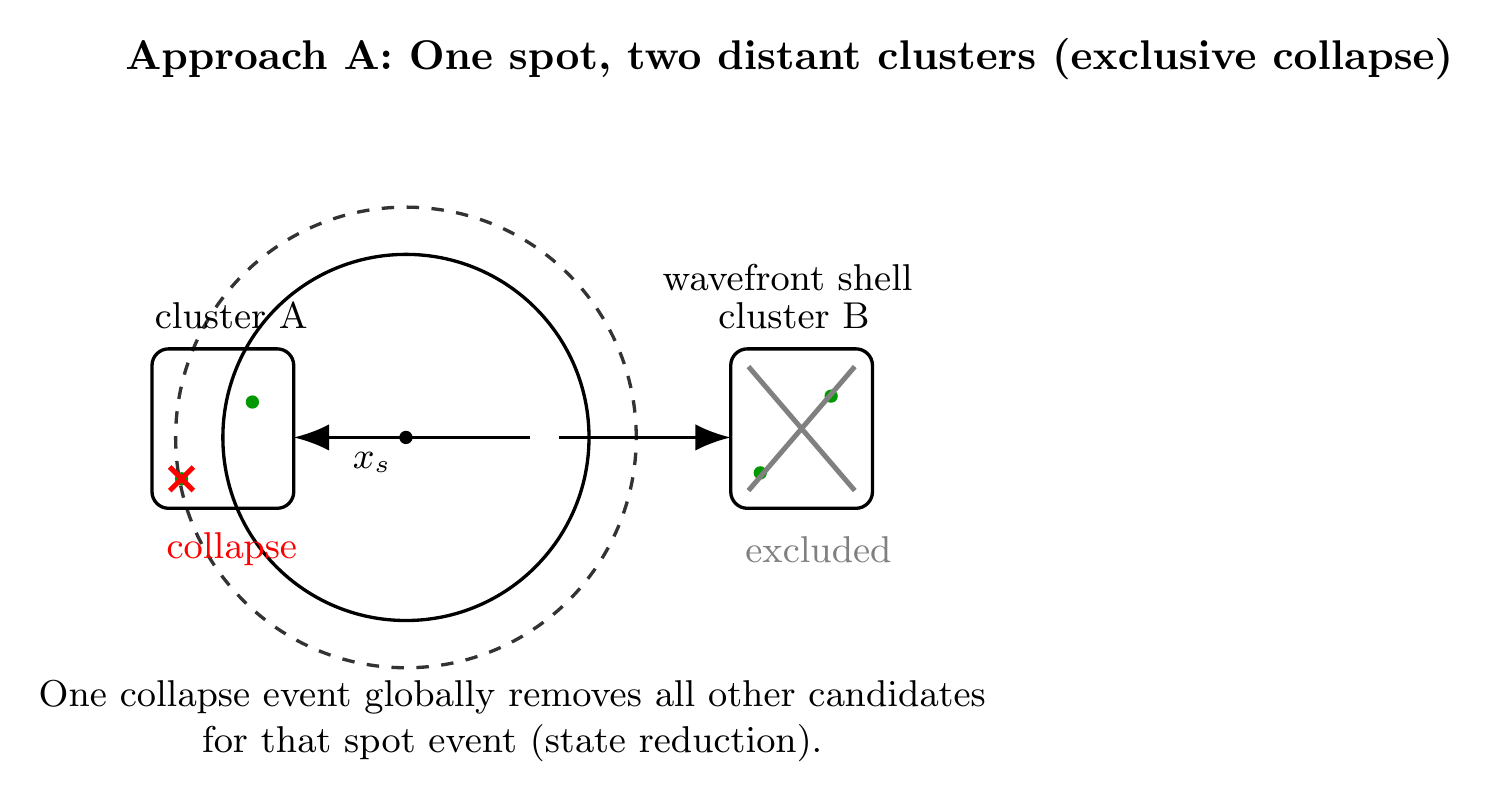
4.1 Two distant clusters on one wavefront
Let A and B be disjoint spatial regions separated by macroscopic distance. Suppose a single spot’s wavefront intersects both regions and both contain ready candidates: Ct = CtA ∪ CtB, with both non-empty. Collapse selects one site X ∈ Ct. If collapse occurs in A, collapse in B is excluded for that event.
4.2 No-signaling
No station can control where collapse occurs. Therefore the instantaneous global candidate update cannot be used for superluminal communication. Nonlocality resides in conditional state descriptions, not in controllable signaling.
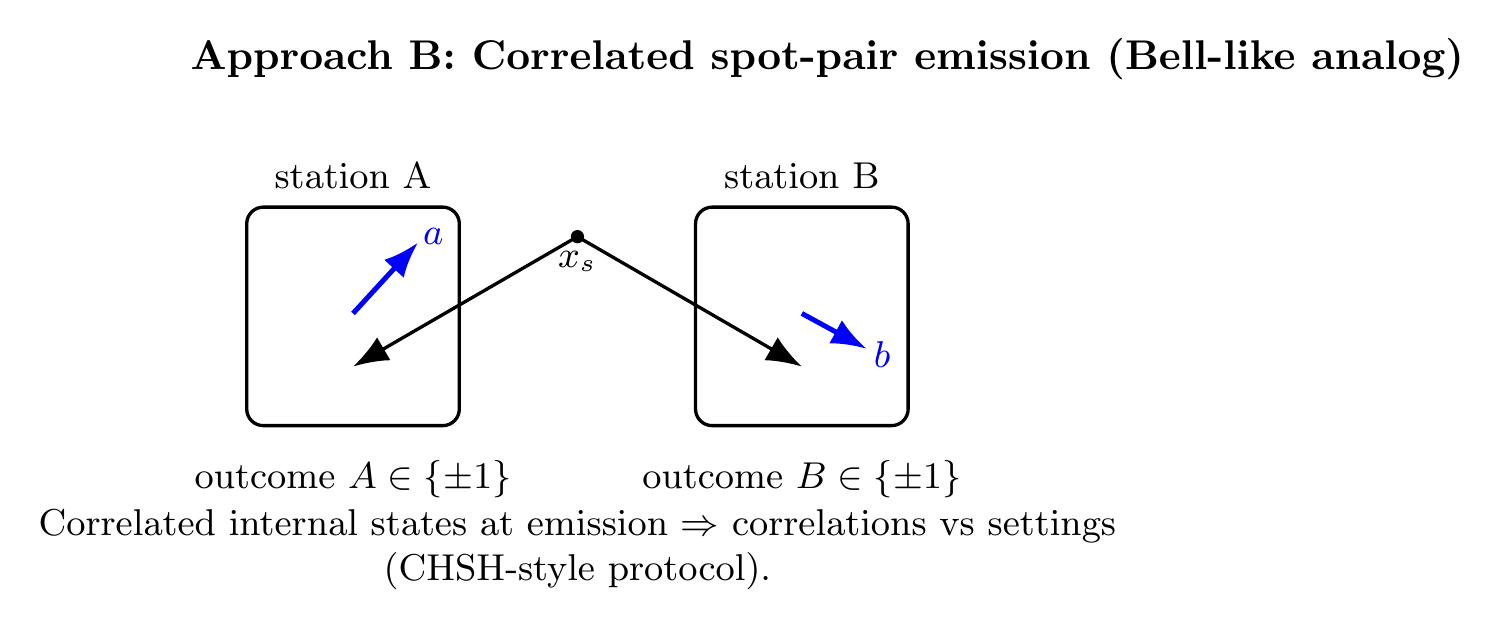
5. Approach B: Correlated Spot-Pair Emission (Bell-Like Analog)
5.1 Correlated pair emission
A local transition at xs emits two spots SA, SB whose internal states are linked. For example, their spin vectors may be anti-correlated: sB = −sA.
5.2 Stations and settings
Each station chooses a setting (measurement basis) by shaping readiness/density masks. A station outputs A(a) ∈ {+1,−1} or B(b) ∈ {+1,−1} depending on which region contains collapse.
6. A CHSH-Style Protocol for EDCA
Repeat trials: emit correlated pair, choose settings a ∈ {a₀,a₁} and b ∈ {b₀,b₁}, evolve until each spot collapses in its station, record outcomes A,B ∈ {±1}. Estimate E(aᵢ,bⱼ) and compute: S = E(a₀,b₀)+E(a₀,b₁)+E(a₁,b₀)−E(a₁,b₁).
Classical local hidden-variable models satisfy |S| ≤ 2, while quantum singlet correlations can reach 2√2. EDCA may or may not exceed 2 depending on collapse weighting and the correlation postulate; this protocol makes it testable.
Interactive toy
Explore the correlated-pair idea interactively: